The standard method of fMRI analysis has been to treat each voxel as an experiment in its own right -- i.e., to apply a parametric statistical test such as a t-test at each voxel independently, and then to correct for the increased liability to false positive results that arises when one makes multiple comparisons.

The usual method of accomplishing this correction is to apply a stringent criterion for tail probability, either calculated as a Bonferroni factor or simply selected arbitrarily.

As Dr Friston detailed earlier, this strategy is suboptimal. It tends to overcompensate for multiple comparisons since it assumes that each test really is independent.

In actuality, activations at separate voxels may be correlated with each other, due to

• spreading activation,
• vascular blurring,
• scanner point spread,
• and functional connectivities between brain regions.

The permutation test that I'll describe automatically takes into account correlations in the data.

As a starting point, I'd like you to consider the case of a single voxel. Forget, for the moment, that this voxel is embedded in a brain and surrounded by many other voxels.

We'd like to evaluate the degree to which the time series of this voxel's intensities in successive images correlates with an ideal waveform describing our experimental task.

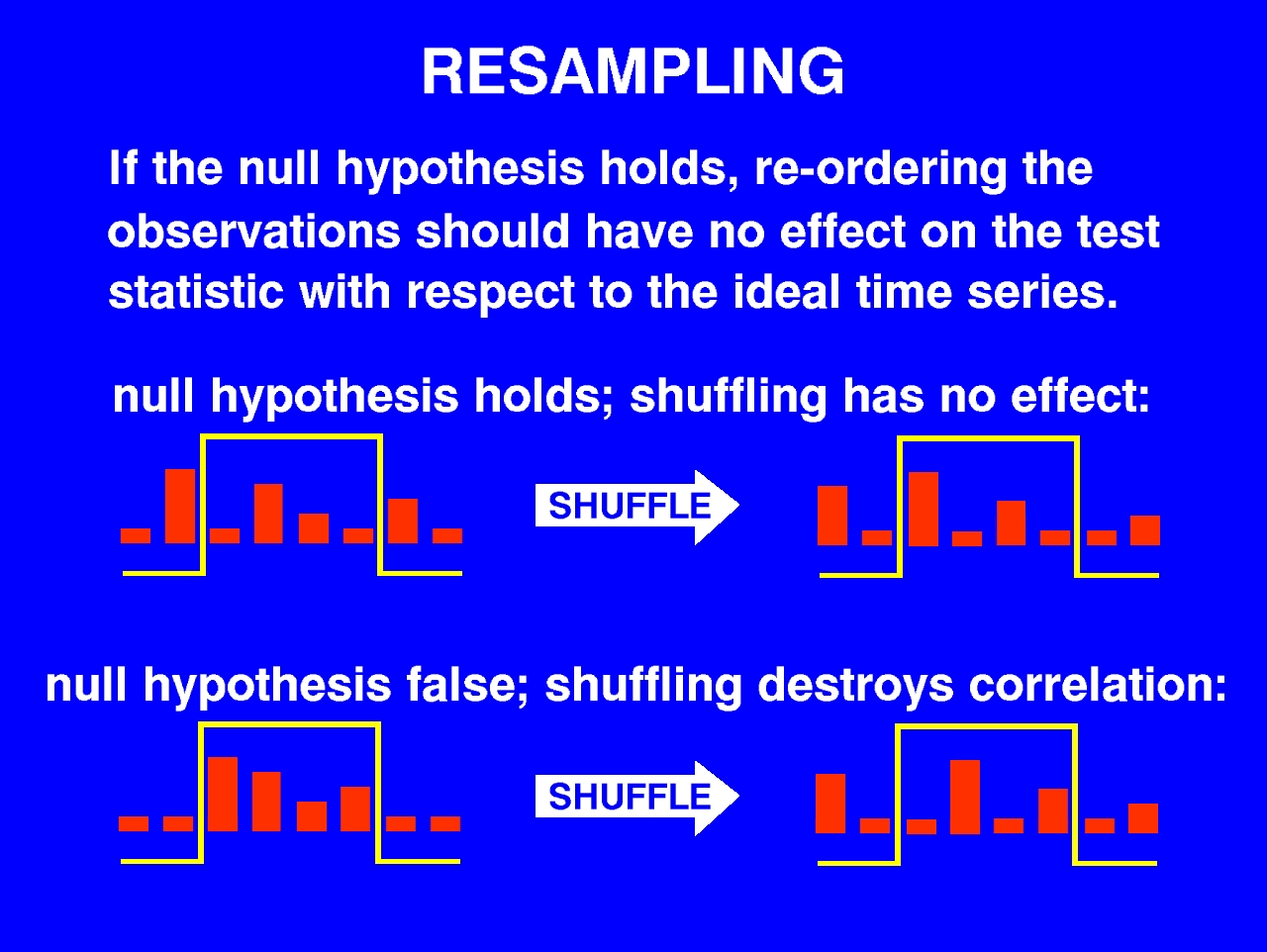
The permutation test depends fundamentally on the fact that if the null hypothesis holds, then re-ordering or `re-sampling' the observations in the time series should on average have no effect on the correlation.

If we shuffle a truly random time series a large number of times, and for each reshuffling take the correlation with our ideal time series, then at the end of this process the set of correlations that we've accumulated is an empirical distribution for the correlation that we could expect to arise by chance. As an alternative to parametric analysis, we can evaluate the tail probability of our observed correlation by ranking it within this empirical distribution.