EXERCISES
Prove the following theorems:
- 0. (P=>(Q=>R))=>(Q=>(P=>R))
- 1. P
 Q=>Q
Q=>Q P (commutativity of
P (commutativity of  )
)
- 2. P
 Q=>Q
Q=>Q P (commutativity of
P (commutativity of  )
)
- 3.
P
 (Q
(Q R)<=>(P
R)<=>(P Q)
Q) (P[[logialand]]R)
(distributivity of
(P[[logialand]]R)
(distributivity of  over
over  )
)
- 4. (P
 Q)
Q) R<=>P
R<=>P (Q
(Q R)
(associativity of
R)
(associativity of  )
)
- 5. (P
 Q)
Q) R<=>P
R<=>P (Q
(Q R)
(associativity of
R)
(associativity of  )
)
- 6. ~(P
 Q)<=>~P
Q)<=>~P ~Q (DeMorgan's
~Q (DeMorgan's
 -Law)
-Law)
- 7. P
 ~P (Law of the Excluded Middle)
~P (Law of the Excluded Middle)
- 8. (P=>Q)<=>~P
 Q (implication reduction)
Q (implication reduction)
- 9. (~P=> false) => P (alternate ~-use rule)
- 10. P
 ~P=>Q (naked contradiction)
~P=>Q (naked contradiction)
- 11. P
 (Q
(Q R) <=>
(P
R) <=>
(P Q)
Q) (P
(P R) (distributivity of
R) (distributivity of
 over
over  )
)
Program Correctness and the Predicate Calculus
Why do we need logic? Formal logic constricts one's thinking, fetters one's
creativity. But formal logic constricts one's thinking to provable statements,
eliminates uncertain reasoning. The argument for formal logic is that of
Mister Spock against Doctor McCoy: certainly we need logical, analytical
thinking, as much as we need its counterpart. If we restrict our reasoning to
formal mathematics but still allow our intuitions to jump outside of the
confines of formal mathematics, then, as Wordsworth said, "the prison unto
which we doom / Ourselves no prison is." Therefore one should not reject
formal logic as dry and boring; it has its place.
My first computer had a forty-column, all-uppercase display and came with a
whopping sixteen kilobytes of memory. Even by current standards, less than ten
years after it was produced, this machine is antiquated. But it served my
purposes. Like most students of programming, I learned haphazardly. I read
the manuals that came with the machine, hacked in BASIC, eventually learned the
assembly language for its microprocessor. I became somewhat renowned locally,
and people began to use my programs. This went on for years, all through high
school, but all the time I was ignorant. I had no idea of what was behind my
programming.
When I wrote a program, I would feel it out by intuition, writing lines of
code as I went along. When I was done I would test it on what I thought were
some representative examples. Often, for any reasonably complex program, I
would find bugs, and then I would go back into the code and fix them. I worked
not so much by pure reasoning as by observation to make my programs correct.
Usually, by the time I finished debugging, my program was as correct as it
would have been had I reasoned it out logically instead of hacking it, though
usually not as clear. But there were some exceptions. When I was in junior
high school a national (but fairly insignificant) computer periodical printed a
short program that I had written to renumber lines of programs written in
BASIC. To be brief, it didn't work. I ended up sending the magazine a letter
of retraction. Of course, they never again accepted anything from me. I had
not reasoned it out, and I had not tested it thoroughly. The design of test
cases is always haphazard; the only way to be sure that a set of test cases is
truly representative of all possible inputs to a program is to analyze the
program logically. And, if one finds it necessary to do that, why not just use
logic to help one design the program correctly in the first place?!
There are many examples of situations in which the use of logic and the
careful consideration of the assumptions upon which one's program depends would
have prevented or corrected significant programming errors. Galaga, a popular
arcade game, is structured as a progression of "levels". On each level, the
player must defend against attackers that enter the screen in a particular
pattern. Upon completion of a level, the level number is incremented and play
proceeds to the level indicated by this number. So a game begins on level 1
and proceeds in order through level 2, level 3, and on up, until all the
player's spaceships have been destroyed by attackers. However, the programmer
of Galaga neglected to note that this program could store only level numbers
from 0 to 255. If you know a little about computer architecture, you see why:
this variable was being stored in a byte, which is eight binary (i.e., base 2)
digits wide. Just as the odometer on a car can record only mileages from 0 to
99 999, a byte can store only numbers in binary from 0 to 11111111, which are 0
to 255 in decimal. The effect of this is that when a player completes level
255, the level number flips to 0. Since 0 is not a legal level number, the
machine cannot find a pattern for it, and appears to become stuck in an endless
loop trying to locate a nonexistent pattern. The only way out of this is to
reinitialise the machine. This bug usually goes unnoticed, because most
players are not proficient enough to reach level 255. I detected this bug in
the summer of 1985. If the programmer had been keeping track of his
assumptions, he would have realised that eight binary digits are not always
sufficient and that therefore either the level number should use more binary
digits or there should be a test in the program that checks whether the level
number has reached 255, and, if so, performs some appropriate action, such as
ending the current game and giving the player a free game with which to
continue playing.
In the fall of 1988, Robert Morris, a first-year graduate student in the
Department of Computer Science at Cornell University, wrote a worm[23] program that was meant to be benign and silent and only
to infiltrate host machines. These machines were parts of the Internet, a
conglomeration of computer networks. Had his program worked as intended, it
would have been a valuable demonstration of the vulnerability of many networked
computers to malicious attack. Unfortunately, Morris was not conscientious in
his implementation. His code contained many bugs, the most serious of which
was in a routine designed to prevent hosts from becoming clogged with multiple
copies of the worm. This part of the program listened for other copies of the
worm running on the same machine, and killed some of them if any were found.
But in the process some copies of the worm were excluded from further killings
and thus became immortal. Also, worms marked for killing did some intensive
computation before terminating and thus loaded down the computer. All these
properties were buried in convoluted and obtuse code, and their deleterious
potential apparently went unnoticed by the author. The worm caused havoc on
the Internet, causing many sites to disconnect themselves in panic and many
people to spend their time attempting to prevent infestation. Morris left the
university shortly afterward and has since been indicted under the Computer
Fraud and Abuse Act. If he had invested time in examining the assumptions
under which his program was operating and the assertions that it established,
he would not have made these errors.
A program can be viewed as a sequence of operations or statements. These
operations can be as simple as hardware-level machine instructions or as
complex as whole subroutines. They alter the state of the machine, that is,
they change the values of variables and alter the flow of control in the
program. In between statements, assertions about the state of the machine can
be made. If one knows the current state, and one is given a statement to be
executed, one can predict the state of the machine after the execution of that
statement. This is the debugging approach: look at the code, find out what's
happening in the machine, and determine how what's happening differs from what
you want to happen. Conversely, if one knows the current state and has
specified the state that is to be established, one can construct a statement or
sequence of statements that will take the machine from here to there, from the
current state to the desired state. This approach is basic to what David Gries
terms "the science of programming". If these logical assertions that express
the state of the machine are constructed at the same time as the statements
that they describe, then the program and the proof of correctness can be
developed hand-in-hand. When the programmer completes this process, they will
have a finished program and a proof of its correctness, and will have spent no
time on debugging. The trade-off, though, is that it takes longer to be
logically meticulous about program statements than it does to blurt out the
program and worry later about correctness. In situations where time is limited
and bugs would not have catastrophic effects, hacking still has its virtues.
However, in abstract algorithms and in programs or modules of programs that
have well-defined tasks, development of proof and program hand-in-hand saves
time and effort.
A logical assertion that is assumed to be true just prior to the execution of
a statement is called the precondition of that statement. If the
statement is executed in a context in which its precondition is true, then it
establishes its postcondition. For example:
precondition: x=42
y := x
postcondition: (x=42) (y=42)
(y=42)
If the postcondition of one statement matches or implies the precondition of
another statement, then those two statements can be chained together into one
compound statement that has the precondition of the first and the postcondition
of the second:
P S0 Q Q S1 R
P S0;S1 R
There are formal systems employing formal logic to prove programs correct, but
the discussion of the application of formal logic to program correctness will
be more informal in this book.
Before treating the use of logical assertions within programs to prove
programs correct, we must extend the propositional calculus. Our extension is
called the predicate calculus, and this name is descriptive. The fundamental
units with which we have been working in the propositional calculus are
sentences, complete propositions. The predicate calculus allows us a finer
resolution. Sentences can be constructed from separate predicates and
subjects. In addition, the predicate calculus allows us to write proofs about
sentences with the wordings "all" and "some". These are called universally
quantified and existentially quantified sentences, respectively. Predicates
are templates that can be attached to a fixed number of subjects. You can
think of a predicate as having a specified number of sockets, each of which can
hold a subject. In order for the predicate to be applied, all the sockets must
be filled by subjects. A predicate having n sockets is called an
n-ary predicate. For example, here is a definition of a unary
predicate:
F(x): x is my friend
`x' is underlined in the sentence in the scheme of abbreviation to show that it
is a placeholder, a marker, for a socket. When a subject is substituted in,
all occurrences of the corresponding placeholder are replaced by the subject.
For example, consider the following scheme of abbreviation, and some
propositions constructed using it:
A : Parmenides F(x) : x says that all is One
B : Zeno G(x, y) : x defends y
H(x) : x is a deconstructionist
I(x) : x is Jacques Derrida
F(A) : Parmenides says that all is One.
G(B, A) : Zeno defends Parmenides.
H(B) : Zeno is a deconstructionist.
H(B) F(A)=>I(B) : If Zeno is a deconstructionist and
Parmenides says that all is One, then Zeno is Jacques Derrida.
F(A)=>I(B) : If Zeno is a deconstructionist and
Parmenides says that all is One, then Zeno is Jacques Derrida.
We now introduce two new symbols, ` ' and `
' and ` ', the
universal and existential quantifiers. A proposition can be quantified by
preceding it with one or more quantifiers. The universal quantifier
`
', the
universal and existential quantifiers. A proposition can be quantified by
preceding it with one or more quantifiers. The universal quantifier
` ' says that any sentence that can be constructed from the
following predicate by substituting the same subject for each occurrence of the
quantified variable is true. This holds for all subjects in the universe.
This is why the universal quantifier is an upside-down `A', meaning "for all".
The existential quantifier `
' says that any sentence that can be constructed from the
following predicate by substituting the same subject for each occurrence of the
quantified variable is true. This holds for all subjects in the universe.
This is why the universal quantifier is an upside-down `A', meaning "for all".
The existential quantifier ` ' says that such a sentence is true
for at least one subject in the universe, but says nothing about which
particular subject it might be. This is why the existential quantifier is a
backwards `E', meaning "there exists". `
' says that such a sentence is true
for at least one subject in the universe, but says nothing about which
particular subject it might be. This is why the existential quantifier is a
backwards `E', meaning "there exists". ` ' and `
' and ` '
have the same precedence as `~', so parentheses must be used to apply them to
sentences that use `
'
have the same precedence as `~', so parentheses must be used to apply them to
sentences that use ` ', `
', ` ', `=>', and `<=>'.
Using the scheme of abbreviation above, we can construct a few examples. (For
simplicity in using these predicates, our universe of discourse here will be
restricted to the set of all people.)
', `=>', and `<=>'.
Using the scheme of abbreviation above, we can construct a few examples. (For
simplicity in using these predicates, our universe of discourse here will be
restricted to the set of all people.)
 xF(x) : Everyone says that all is One.
xF(x) : Everyone says that all is One.
 xG(x, A) : Someone defends Parmenides.
xG(x, A) : Someone defends Parmenides.
 xG(A, x) : Parmenides defends someone.
xG(A, x) : Parmenides defends someone.
 x(H(x)=>F(x)) : All deconstructionists say that all is One.
x(H(x)=>F(x)) : All deconstructionists say that all is One.
 x(H(x)
x(H(x) ~F(x)) : There is some deconstructionist
who does not say that all is One.
~F(x)) : There is some deconstructionist
who does not say that all is One.
 x
x yG(x, y) : Someone defends everyone. (That is,
there is some one particular person who defends everybody.)
yG(x, y) : Someone defends everyone. (That is,
there is some one particular person who defends everybody.)
 x
x yG(y, x) : Everyone defends someone. (That is,
there is some one particular person who is defended by everyone. Sort of like
Oliver North.)
yG(y, x) : Everyone defends someone. (That is,
there is some one particular person who is defended by everyone. Sort of like
Oliver North.)
 x
x yG(x, y) : Everyone defends someone. (The person
being defended can be a different person for each defender.)
yG(x, y) : Everyone defends someone. (The person
being defended can be a different person for each defender.)
The final three examples above demonstrate the potential for ambiguity in
natural languages even when describing very simple quantifications. You should
be wary of such ambiguities when translating between a natural language and
logical notation, and when you are thinking in a natural language.
As in the fourth and fifth examples above, `=>' is often used with
` ' and `
' and ` ' with `
' with ` ' to restrict the
scope of a quantification. In a proposition of the form
' to restrict the
scope of a quantification. In a proposition of the form
 x(G(x)=>H(x)), the antecedent can be thought of as a gate or a
guard. For all subjects x, if x satisfies the guard G, then it
must satisfy the predicate H. However, if x does not satisfy G, then no
assertion about it is made; it escapes the quantification. Similarly, in a
proposition of the form
x(G(x)=>H(x)), the antecedent can be thought of as a gate or a
guard. For all subjects x, if x satisfies the guard G, then it
must satisfy the predicate H. However, if x does not satisfy G, then no
assertion about it is made; it escapes the quantification. Similarly, in a
proposition of the form  x(G(x)
x(G(x) H(x)), where G is
some identifying property such as "is a deconstructionist", the application of
H is restricted to those subjects that satisfy G. It is a mistake to confuse
the symbols involved in these two cases. Think about the meanings of
propositions of the forms
H(x)), where G is
some identifying property such as "is a deconstructionist", the application of
H is restricted to those subjects that satisfy G. It is a mistake to confuse
the symbols involved in these two cases. Think about the meanings of
propositions of the forms  x(G(x)=>H(x)) and
x(G(x)=>H(x)) and
 x(G(x)
x(G(x) H(x)), and recognise this.
H(x)), and recognise this.
A variable that occurs next to a quantifier is said to be bound within
the quantified expression. Variables that are not bound within an expression
are free. So, for example, in the proposition  yG(x, y),
x is free and y is bound. (The possibility of unbound variables
will be discussed shortly.) These definitions are important in what follows.
To make derivations using quantifiers, we introduce two new derivation rules
and two proof techniques.
yG(x, y),
x is free and y is bound. (The possibility of unbound variables
will be discussed shortly.) These definitions are important in what follows.
To make derivations using quantifiers, we introduce two new derivation rules
and two proof techniques.


proof: F(k), where k is arbitrary F(A)
 xF(x)
xF(x)  xF(x)
xF(x)
use:  xF(x)
xF(x)  xF(x)
xF(x)
F(A) F(k), where k is arbitrary
The  -use rule states that if it is known that a predicate (that
is, either an atomic predicate or a compound proposition in which one or more
variables are bound) is true for all subjects, then it can be derived that that
predicate is true for any particular subject. This is a weakening of the
original assertion, since although
-use rule states that if it is known that a predicate (that
is, either an atomic predicate or a compound proposition in which one or more
variables are bound) is true for all subjects, then it can be derived that that
predicate is true for any particular subject. This is a weakening of the
original assertion, since although  xF(x) => F(A), ~(F(A) =>
xF(x) => F(A), ~(F(A) =>
 xF(x)). The
xF(x)). The  -proof rule states that if it is known
that a predicate is true for a particular subject, then it can be derived that
that predicate is true for some (unspecified) subject. Again, this is a
weakening of the assertion, since the derived proposition holds no information
about which particular subject or subjects the predicate applies to. The other
two rules are more complicated. The
-proof rule states that if it is known
that a predicate is true for a particular subject, then it can be derived that
that predicate is true for some (unspecified) subject. Again, this is a
weakening of the assertion, since the derived proposition holds no information
about which particular subject or subjects the predicate applies to. The other
two rules are more complicated. The  -proof rule states that if a
property can be proven for an arbitrary subject, then that property holds for
all subjects. What we mean by "arbitrary subject" is a subject that has no
special, distinguishing properties. For if a property can be proven for a
subject that is so plain-vanilla that it could be any subject, then,
intuitively, that property holds for all subjects. Formally, what we mean by
"arbitrary" is that the variable shall not have occurred anywhere in the proof
up until the point at which it is introduced as arbitrary. For if no
proposition contains the variable, then we cannot possibly have any information
about it, and therefore it is arbitrary, a tabula rasa. Note that this
arbitrary variable is unbound. The
-proof rule states that if a
property can be proven for an arbitrary subject, then that property holds for
all subjects. What we mean by "arbitrary subject" is a subject that has no
special, distinguishing properties. For if a property can be proven for a
subject that is so plain-vanilla that it could be any subject, then,
intuitively, that property holds for all subjects. Formally, what we mean by
"arbitrary" is that the variable shall not have occurred anywhere in the proof
up until the point at which it is introduced as arbitrary. For if no
proposition contains the variable, then we cannot possibly have any information
about it, and therefore it is arbitrary, a tabula rasa. Note that this
arbitrary variable is unbound. The  -use rule states that if it
is known that a property F holds for some subject, then that unknown subject
can be given a name, in the form of an arbitrary variable. Again, in order for
this rule to be valid, the variable that is introduced by it must not have
occurred before anywhere within the proof.
-use rule states that if it
is known that a property F holds for some subject, then that unknown subject
can be given a name, in the form of an arbitrary variable. Again, in order for
this rule to be valid, the variable that is introduced by it must not have
occurred before anywhere within the proof.
For the purposes of the present discussion, it is sufficient that the reader
understand how to write expressions in the predicate calculus; it is not
necessary to know how to construct proofs in the predicate calculus. For those
who are interested, we briefly present one sample proof and a few exercises.
More may be found in any text on elementary logic.
Show ~ xF(x) <=>
xF(x) <=>  x~F(x)
x~F(x)
0. [assume ~ xF(x) Show
xF(x) Show  x~F(x)
x~F(x)
1. [assume ~ x~F(x) Show false
x~F(x) Show false
2. [assume ~F(k) Show false
3.  x~F(x)
x~F(x)  -proof, 2
-proof, 2
4. false ] false-proof, 3, 1
5. ~F(k)=>false =>-proof, 2..4
6. ~~F(k) ~-proof, 5
7. F(k) ~-use, 6
8.  xF(x)
xF(x)  -proof, 7
-proof, 7
9. false ] false-proof, 8, 0
10. ~ x~F(x)=>false =>-proof, 1..9
x~F(x)=>false =>-proof, 1..9
11. ~~ x~F(x) ~-proof, 10
x~F(x) ~-proof, 10
12.  x~F(x) ] ~-use, 11
x~F(x) ] ~-use, 11
13. ~ xF(x) =>
xF(x) =>  x~F(x) =>-proof, 0..12
x~F(x) =>-proof, 0..12
14. [assume  x~F(x) Show ~
x~F(x) Show ~ xF(x)
xF(x)
15. ~F(y)  -use, 14
-use, 14
16. [assume  xF(x) Show false
xF(x) Show false
17. F(y)  -use, 15
-use, 15
18. false ] false-proof, 17, 15
19.  xF(x)=>false =>-proof, 16..18
xF(x)=>false =>-proof, 16..18
20. ~ xF(x) ] ~-proof, 19
xF(x) ] ~-proof, 19
21.  x~F(x) => ~
x~F(x) => ~ xF(x) =>-proof, 14..20
xF(x) =>-proof, 14..20
22. ~ xF(x) <=>
xF(x) <=>  x~F(x) <=>-proof, 13,
21
x~F(x) <=>-proof, 13,
21
EXERCISES
0. Prove that ~ xF(x) <=>
xF(x) <=>  x~F(x).
x~F(x).
In exercises 1 to 5, let the universe of discourse be the set of all people,
let L(x, y) denote "x loves y", and let A, B, and C be people.
Express the given propositions in the language of the predicate calculus.
- 1. A loves everyone who loves her.
- 2. B loves himself.
- 3. Exactly one person loves A.
- 4. Nobody except B loves B.
- 5. Nobody loves anyone who loves themselves.
6. What seems strange about the proposition in exercise 5?
Proving Loops Correct
The iteration statement or loop is a common programming language construct.
Being so common, it is all too often taken for granted. A logical
formalisation of loops can guide the programmer in the construction of loops,
and make them clearer and more efficient. We have already seen how statements
accompanied by preconditions and postconditions can be concatenated by matching
up the conditions, and how, given a pair of conditions, a sequence of
statements can be constructed to accomplish the transition from one condition
to the other. Now we will examine correctness proofs for loops.
Like all statements, the loop has a precondition and a postcondition. There
are also two other conditions associated with a loop. These are the
invariant and the guard. The invariant is an assertion in terms
of the loop variables that is always true at the beginning and at the end of
every iteration; it is both a precondition and a postcondition of the sequence
of statements that constitutes the loop body. The name is logical; the truth
of the invariant does not vary from one iteration to the next. Execution of a
loop begins at the beginning of the first iteration. Since the invariant must
be true at the beginning and at the end of every iteration, and in particular
at the beginning of the first iteration, it follows from this that the
precondition of the loop must imply the invariant. The precondition is
established by statements preceding the loop itself that initialise the loop's
variables. The guard is so called because it decides whether or not the loop
will continue on to another iteration; it guards entry to the loop body. The
guard is evaluated before every iteration, and when it is false, the loop
terminates. As well as these conditions, there is a decreasing bound
function, a function of the loop's variables that yields an upper bound on
the number of iterations yet to be executed. (An upper bound on a
function f is simply a function b such that
b(x)>f(x) for all values of x, even if the precise
value of f(x) cannot be determined.) If the bound function is
decreasing on every iteration, then it must eventually reach zero. Since every
non-negative function that is bounded by zero must itself be zero, this
requirement ensures that the loop eventually terminates instead of executing
infinitely. Invariants and bound functions may refer both to explicit
variables and to implicit variables. By "implicit variables" are meant
abstract variables whose values are unknown at the time that the algorithm is
being defined, such as "the number of characters yet to be typed in by the
user" or "the number of days between now and September 13th,
1999". This is permitted because the invariant and the
bound function are abstract statements; a Pascal compiler, for example, does
not need to know about them, and therefore they need not be phrased explicitly.
Here is the general form of a loop, with the assertions labelled with letters
and appearing in the locations in which they must hold:
...initialiasation...
precondition: Q
do B ->
invariant and guard: P B
B
...loop body...
invariant: P
od
postcondition: R
Here is the same general form of a loop, expressed in the Pascal programming
language:
...initialisation...
precondition: Q
while B do
begin
invariant and guard: P B
B
...loop body...
invariant: P
end
postcondition: R
Note that the assertions that do not constitute part of the language's syntax
(i.e., all except the guard, in the Pascal language) must be expressed as
comments. When annotating programs, each condition is written only once, in
order to save space and to eliminate confusion. So a fully annotated loop in
Pascal has the following form:
...initialisation...
precondition: Q
invariant: P
bound: b
while B do
begin
...loop body...
end
postcondition: R
Often, the precondition and the postcondition will be obvious from the
invariant. In such situations, they may be omitted. Some loops are so trivial
that they need not be annotated at all. A loop that initialises an array by
reading in all its elements, for example, is trivial. There are two main
considerations in deciding what amount of annotation should be used for any
given loop: The loop should be made logically understandable, but, at the same
time, the annotation should not clutter the scene so much that it becomes
confusing. The more you program, the better your sense of balance between
these two forces will become.
Note that the precondition of the loop body must be (implied by) the
conjunction of the invariant and the guard, since these are the conditions that
are true at the beginning of every iteration. Similarly, the invariant must be
the postcondition of the loop body, because it is true at the end of every
iteration. A loop is correct if and only if the following relationships
hold:
- The precondition implies the invariant: Q=>P
- The sequence of statements that constitutes the loop body is correct:
P
 B ...loop body... P
B ...loop body... P
- The conjunction of the negation of the guard and the invariant implies the
postcondition: P
 ~B=>R
~B=>R
- There is a decreasing bound function.
The best approach is not to write the entire loop and only then to verify that
these conditions hold, but to develop the conditions and the relationships
among them as the loop is being conceived. As one begins to write the loop,
the postcondition and some form of precondition are already fixed; they are
dictated by the problem definition. The first step is to develop the
invariant. This should be accomplished by weakening the postcondition. We
know that we want the invariant to imply the postcondition when combined with
the negation of the guard, so it is reasonable to form the invariant by
weakening that postcondition. Thus the invariant can be viewed as a compromise
between the precondition and the postcondition. Gries[24]
describes four general methods for weakening a postcondition. These include
replacing a constant in the postcondition by a loop variable or a function of
the loop variables, enlarging the range of a variable from the range specified
in the postcondition, deleting a conjunct from the postcondition, and
combination methods. Since the precondition of the loop must imply the
invariant, a loop initialisation should be constructed that sets up the loop
variables so that the invariant is established by the time the loop is
entered.
A loop solves a problem by taking small bites out of it until the whole
problem has been digested. We can make this case literal with our first
example. Suppose that one is faced with the problem of eating a hamburger that
can be divided into NumBites separate bites, numbered from 0 to NumBites-1. We
are given the operation TakeBite(k), which takes the kth
bite of the burger. We want to write a loop whose
precondition is that the whole burger is sitting on the plate and whose
postcondition is that the whole burger has been eaten. An obvious compromise
between these two conditions is that part of the burger has been eaten. More
formally, we define a variable k such that at the beginning and at the
end of every iteration, the first k bites of the burger have been eaten.
We want a guard whose negation, when combined with this invariant, implies the
postcondition. The obvious choice for this guard is that k does not
equal NumBites, for when the negation of this is true (i.e., k does
equal NumBites), then the invariant states that all NumBites bites in the
burger have been eaten. A simple bound function for this loop is
NumBites-k. Here is the complete loop. Note that the two statements
that constitute the loop body are written to accomplish the operations of
decreasing the bound function and maintaining the invariant.
k := 0;
precondition: The burger is uneaten, (i.e., 0 bites have been eaten), and
k = 0.
invariant: The first k bites of the burger have been eaten.
bound: NumBites-k
do k!=NumBites ->
TakeBite(k);
k := k+1
od
postcondition: The entire burger has been eaten. (i.e., all bites have been
eaten.)
I have taught many students who feel uncomfortable with and even hostile to
the notion of loop invariants simply because they do not properly understand
the nature of loop invariants. I will try here to prevent the development of
some common misconceptions. If you pay close attention to only one small
portion of this section, let it be these two paragraphs. The invariant is a
condition. It is not a command; its nature is declarative, not imperative. "x
:= 0" cannot be an invariant, but "0<=x<42" can. I have had some
students who, when asked to write an invariant, wrote a narrative description
of what the loop was doing, such as this attempt at an invariant which occurred
in a lexical scanner, in a loop whose function was to read in a string of
numeric characters and construct the integer represented by them: "Start with
CurrentCharacter in ['0'..'9'] and NumberValue = 0. Add each digit in the
input onto the end of NumberValue. Stop when CurrentCharacter is no longer a
digit." This is an adequate description of what the loop is doing, but it is
not an invariant. It is rather a muddled combination of precondition,
invariant, guard, and postcondition. The invariant in this case is "The prefix
of the digit string that has been scanned so far is the decimal representation
of NumberValue". The corresponding loop looks like this:
NumberValue := 0;
do CurrentCharacter  '0'..'9' ->
'0'..'9' ->
NumberValue := NumberValue.10 + (ord(CurrentCharacter) - ord('0'));
CurrentCharacter := ReadNextCharacter()
od
The guard is that CurrentCharacter is a digit. Initially, the prefix is the
null string (i.e., the string that comprises zero characters), because none of
the digits have been scanned, and the corresponding accumulated value in
NumberValue is 0. (We assume for simplicity that the null string is a valid
representation for the number 0.) When the guard becomes false, all the digits
have been scanned, so the current prefix is the entire digit string, and so the
invariant says that NumberValue must be the value whose decimal representation
is the entire digit string. This is the postcondition.
In order for the invariant to be relevant to the loop, it must be phrased in
terms of the loop variables. "The sky is blue" is certainly invariant, in that
it is always true at the beginning and at the end of every iteration of a loop.
But such an invariant, one that is true for any loop, has nothing to say about
how a particular loop should be constructed. Remember that you can use
implicit loop variables as well as explicit ones in defining the invariant.
Because the invariant makes a general statement about every iteration of a
loop, you should avoid special cases and words such as "except" in defining
invariants. If these occur, they are probably telling you that there is a
simpler way of writing the loop than the one that you are thinking of.
For another example, suppose I want to write a loop to print the squares of
the integers from 0 to 9. The precondition of the initialisation is simply
"true", a dummy precondition that asserts nothing. The postcondition of the
loop is "the squares of all the integers from 0 to 9 have been printed". A
good way to weaken the postcondition in this case seems to be to replace the
constant 9 by a loop variable, which we will call i. This yields the
invariant "the squares of all the integers from 0 to i-1 have been
printed". (Since it is more natural to let i start out at 0 instead of
at -1, we choose this form of the invariant over the more naïve `the
squares of all the integers from 0 to i have been printed", along with
the appropriate initialisation i := 0 instead of i := -1.) The guard is
dictated by the way in which the postcondition has been weakened; we know that
its negation when combined with the invariant must imply the postcondition, so
the guard must be i!=10. It remains to write the body of the loop.
This should always be done last. The loop body has two goals: to decrease a
bound function, and then to reestablish the invariant, which may have been
violated when the bound function was decreased. (Remember, it is only at the
beginning and at the end of each iteration that the invariant must be true. It
can become false in the middle of the loop body, as long as it is reestablished
by the end of the loop body.) A suitable bound function here is i-10
along with an increment statement i := i+1 in the loop body to decrease it.
This is the tightest possible bound; it gives exactly the number of iterations
remaining. Bound functions are not always as precise as this. If i is
increased and nothing else is changed, the invariant no longer holds; the
(i-1)th square has not yet been printed. The invariant
can be reestablished by a statement that prints that square. So the full loop,
with initialisation, is this:
i := 0;
precondition: i=0, and no squares have been printed
invariant:  k(0<=k<i => k2 has been
printed)
k(0<=k<i => k2 has been
printed)
bound: i-10
do i != 10 ->
write(i2);
i := i+1
od
postcondition:  i(0<=i<10 => i2
has been printed)
i(0<=i<10 => i2
has been printed)
The "Russian peasant" multiplication algorithm is a simple way of implementing
multiplication using the two simpler operations add and shift. It is used in
some electronic calculators. A shift operation is a simple way of multiplying
or dividing a binary number by two. A left shift moves all the digits left one
place and concatenates a 0 on the right. A right shift moves all the digits
right one place, dropping the rightmost digit. A left shift in decimal
representation multiplies by ten, and a right shift in decimal representation
divides by ten. (If the number is not a multiple of ten, then the remainder
from the division is discarded.) 42 when shifted left becomes 420. 54 when
shifted right becomes 5. Similarly, the binary number 11 (3 in decimal) when
shifted left becomes 110 (6=3.2), and when shifted right becomes 1. The
Russian peasant algorithm can be implemented as a loop, and to find its
invariant we combine the precondition and the postcondition of the problem.
The precondition is that we are given two numbers a, b whose product we
must find. The postcondition is that we have found one number s that is
the product. A natural compromise between these two situations is that we have
three quantities x, y, s such that xy+s is the product. To
establish this invariant at the beginning of the algorithm, we can make the
initial values of x and y the two multiplicands, and set s
to 0:
the multiplicands a, b have been provided by another part of the
program
x := a;
y := b;
s := 0;
precondition: (xy = ab)  (s = 0)
(s = 0)
invariant: xy+s = ab
<...loop...>
postcondition: s = ab
So, although we have yet to do any work on the computation, the invariant holds
at the beginning of the first iteration of the loop, because xy+0 is
indeed the product. Given the invariant, the postcondition will be established
when xy = 0, so the loop guard must be xy != 0. In fact, x,
not y, is the number that our algorithm will cause to become 0, so
we can simplify the guard to x != 0. (Since the problem is symmetric in
x and y (i.e., xy is the same number as yx), we could just as
well have constructed the algorithm so that y goes to 0 instead of x.
The choice is arbitrary.) A bound function for the loop is the value of
x. The body of the loop must decrease the bound function while
maintaining the invariant. Here it is. (We assume the existence of functions
ShiftLeft and ShiftRight, which perform the left and right shift operations on
their arguments, and RightmostBit, which returns the rightmost binary digit of
its argument.)
the multiplicands a, b have been provided by another part of the
program
x := a;
y := b;
s := 0;
precondition: (xy = ab)  (s = 0)
(s = 0)
invariant: xy+s = ab
bound: x
do x != 0 ->
if RightmostBit(x) = 0 ->
x := ShiftRight(x);
y := ShiftLeft(y)
[] RightmostBit(x) = 1 ->
s := s+y;
x := x-1
fi
od
postcondition: s = ab
The loop body is an alternative statement containing two cases, each of which
decreases the bound function while maintaining the invariant. (In Pascal, this
statement would have the form "if RightmostBit(x) = 0 then
... else ...", with one case under the "then" and the other under the
"else".) If the rightmost binary digit of x is 0, then x is
shifted right (divided by two), y is shifted left (multiplied by two),
and s is left unchanged. Dividing x by two and multiplying
y by two does not alter the product xy, so the invariant is
maintained. At the same time, the bound function x is decreased. If
the rightmost binary digit of x is 1, then it is changed to 0, and y
is added to s. Changing the rightmost digit from a 1 to a 0
decreases x by 1, so this takes care of the requirement that the bound
function be decreased. The invariant is maintained, because
(x-1)y + (s+y) has the same value as the original
expression xy+s. Therefore, the loop is correct.
A real-world example from my own golden age of hacking hopefully will serve to
convince the reader of the general applicability of this technique of
developing a loop. Digital sampling is a technique that occurs in applications
from user interfaces to process controls to digital music. The
analog-to-digital converter is a basic device of digital sampling; it produces
a number in a predefined, bounded range corresponding to the level of some
analog input parameter. For reasons of hardware, it is cheaper and easier to
build a hardware digital-to-analog converter (DAC) than it is to build a
hardware analog-to-digital converter (ADC). To economise, it is possible to
implement an ADC using a DAC and a comparator. A comparator compares
two analog input voltages, V0 and V1. Its1-bit digital output is a low voltage
if V0<=V1, and a high voltage if V0>V1.
* Thinking of the DAC and the comparator as functional "black boxes", that is,
as computational entities with only inputs and outputs whose internals are
irrelevant, how would you connect their inputs and outputs to build a
higher-order black box that compares an analog input with a digital input?
(You may wish to draw a diagram.)
* Give an algorithm that uses your new black box to implement an ADC. You
should work out your own solution and then examine the one given here. You may
make the following assumptions:
* The digital value corresponding to the analog level is in the range
[0..MAXLEVEL].
* The output of your black box can be read by your program as the value of
the Boolean variable comparator, where the value true corresponds
to a high voltage and false to a low voltage.
* The input of the DAC comes from the integer variable dac_input.
* The comparator and the DAC function instantaneously; there is no need to
wait in between setting their inputs and reading their outputs.
* The level of the input is constant during the execution of your
algorithm.
The solution here uses a general technique called binary search in which
the range of uncertainty is halved on each iteration of the loop. In this
context of determining a value given only "higher" or "lower" responses to
one's guesses, the strategy of binary search is often referred to as
successive approximation. If I am to guess a whole number based on
responses of "higher" or "lower", and initially I know that this number N lies
in a range 0<=N<2E, there is a strategy that allows
me to arrive at N within a maximum of E+1 guesses. The postcondition here is
that we have correctly guessed N. This condition can be viewed as the state of
having pinched down a range of uncertainty so that it comprises only one
number. The invariant, then, is arrived at by the method of enlarging the
range of a variable. The range is bounded as follows:
0 <= lower_bound <= voltage < upper_bound <= 2E
This invariant can be established using the initialisation
lower_bound := 0; upper_bound := 2E
Given the invariant, the range will have converged to a single value when the
upper bound is just above the lower bound. The guard, then, is
upper_bound != lower_bound+1
A loose but adequate bound function is one less than the number of values still
left in the range of uncertainty:
b = upper_bound-lower_bound-1
The body of the loop follows. To decrease the interval of uncertainty and
thereby decrease the bound function, we guess the average of the two bounds and
feed that guess through the DAC to the comparator. Using the output of the
comparator we discard half the interval. (This example assumes that the output
of the DAC is connected to the V0 input of the comparator, and that the analog
voltage input is connected directly to the V1 input of the comparator.) In
this way we converge logarithmically upon the digital value that corresponds to
the input voltage level. Here is the algorithm in full:
lower_bound := 0; upper_bound := 2E;
invariant: 0 <= lower_bound <= voltage < upper_bound <= 2E
bound: upper_bound-lower_bound-1
do upper_bound != lower_bound+1 ->
dac_input := (lower_bound + upper_bound)/2;
if comparator -> upper_bound := dac_input
[] ~comparator -> lower_bound := dac_input
fi
od
postcondition: voltage = lower_bound
As mathematicians are wont to do, in solving this problem we made a
simplifying assumption that is not quite true in the real world. To phrase it
more bluntly, we cheated. The input level is not necessarily constant while
the program is running. In fact, if it is an audio or other oscillatory signal
that is being digitised, the input is certainly changing during the execution
of the algorithm. How does this fact affect the accuracy of the algorithm
presented above? (Think about the process by which the interval is shrunken.)
How does it affect the accuracy of your own algorithm? For both algorithms,
think on the following questions: Does the algorithm produce a value that is
the correct digital representation of the signal at the moment at which the
algorithm terminates? If not, what can you assert about the result
of the algorithm? Given a fast enough computer upon which to execute, will the
algorithm still work in practice?
This concludes our brief discussion on developing correct programs. Excellent
further reading on this subject is [Gries 1981].
Induction
A line of dominoes is set up so that when any domino falls, it causes its
successor to fall. The first domino is knocked over.
If a climber can reach a rung of a ladder, then they can reach the rung after
it. The climber can reach the first rung of the ladder.
If a unit of water flows out of a siphon, the next unit of water will be drawn
up into its place and will also flow out of the siphon. The first unit of
water is drawn out of the siphon. For any n, if predicate F is true for
all natural numbers less than n, then F is true for n (i.e.,
 n(
n( k(k < n =>
F(k)) => F(n))). F is true for subject 0 (i.e., F(0)).
k(k < n =>
F(k)) => F(n))). F is true for subject 0 (i.e., F(0)).
The above four cases are similar. We infer on an intuitive level that all the
dominoes fall, that the climber can reach all the rungs of the ladder, that all
the water flows out of the siphon, and that F is true for all natural numbers
( nF(n)). Each of these arguments rests upon the
notion of induction. Induction, in general, is a process of going from
specifics to universalities. Given the specifics that one falling domino
causes the next domino to fall and that the first domino does fall, one can
induce the universality that all the dominoes fall. Given the specifics that
if a particular property holds for a natural number then it holds for the next
natural number and that the property holds for a particular natural number
k, one can induce the universality that it holds for all natural numbers
greater than or equal to k. In general, given the specifics that if a
particular property holds for a subject in some ordering then it holds for the
next subject(s) in the ordering and that the property holds for some particular
subject k in the ordering, one can induce the universality that it holds
for all subjects in the ordering that are direct or indirect successors of
k. (A subject can have more than one predecessor and/or more than one
successor. Natural numbers have unique predecessors and successors because
they constitute a special kind of ordering called a linear ordering.
But arrangements of subjects need not be linear. They can contain branches
and joins, just as a chain of dominoes can contain branches and joins.) An
inductive proof consists of a base case and an inductive step.
The base case is the first domino, the bottom rung of the ladder, the base
upon which the chain of implication is founded. Usually most of the work in an
inductive proof happens in the inductive step. This step is a universally
quantified implication that moves the property from k to the
successor(s) of k. It is proven either by
nF(n)). Each of these arguments rests upon the
notion of induction. Induction, in general, is a process of going from
specifics to universalities. Given the specifics that one falling domino
causes the next domino to fall and that the first domino does fall, one can
induce the universality that all the dominoes fall. Given the specifics that
if a particular property holds for a natural number then it holds for the next
natural number and that the property holds for a particular natural number
k, one can induce the universality that it holds for all natural numbers
greater than or equal to k. In general, given the specifics that if a
particular property holds for a subject in some ordering then it holds for the
next subject(s) in the ordering and that the property holds for some particular
subject k in the ordering, one can induce the universality that it holds
for all subjects in the ordering that are direct or indirect successors of
k. (A subject can have more than one predecessor and/or more than one
successor. Natural numbers have unique predecessors and successors because
they constitute a special kind of ordering called a linear ordering.
But arrangements of subjects need not be linear. They can contain branches
and joins, just as a chain of dominoes can contain branches and joins.) An
inductive proof consists of a base case and an inductive step.
The base case is the first domino, the bottom rung of the ladder, the base
upon which the chain of implication is founded. Usually most of the work in an
inductive proof happens in the inductive step. This step is a universally
quantified implication that moves the property from k to the
successor(s) of k. It is proven either by  -proof or by
another induction.
-proof or by
another induction.
There are two forms of induction. In strong induction, the inductive
case takes as its antecedent the fact that all subjects in the ordering that
are less than the particular subject k possess the property in question.
Sometimes this much information is necessary in order to prove that the
property holds for k. In many interesting cases, however, the only
information needed is that the property holds for the immediate predecessor(s)
of k. This is called weak induction. This text will treat only
weak induction. The rules for inductive proof may be summarised as follows:
weak induction: F(n)  k(F(k) => F(k+1)) strong
induction: F(n)
k(F(k) => F(k+1)) strong
induction: F(n)  k(
k( m(n<=m<k => F(m))
=> F(k))
m(n<=m<k => F(m))
=> F(k))
 x(x>=n => F(x))
x(x>=n => F(x))
 x(x>=n => F(x))
x(x>=n => F(x))
Here is a sample inductive proof about summations. Algebraic details have
been eliminated and reasons have been omitted for brevity. In an inductive
proof, the assumption for =>-proof is called the inductive hypothesis.
Many presentations of inductive proofs omit the final step that uses the
=>-proof rule and simply understand it to be present, but in this book it is
included in order to make the technique more obvious for beginners.
Show  n(
n( i = (n)(n+1)/2) by
weak induction:
i = (n)(n+1)/2) by
weak induction:
base case:
 [i=0,0] i = 0
[i=0,0] i = 0
= (0)(0+1)/2
inductive case:
[assume  [i=0,k]i = (k)(k+1)/2 Show
[i=0,k]i = (k)(k+1)/2 Show  [i=0,k+1] i
= (k+1)((k+1)+1)/2
[i=0,k+1] i
= (k+1)((k+1)+1)/2
 [i=0,k+1] i =
[i=0,k+1] i =  [i=0,k]
i + (k+1)
[i=0,k]
i + (k+1)
= (k)(k+1)/2 + (k+1) from the inductive hypothesis
= (k2 + 3k + 2)/2
= (k+1)(k+2)/2
= (k+1)((k+1)+1)/2 ]
 [i=0,k] i = (k)(k+1)/2 =>
[i=0,k] i = (k)(k+1)/2 =>  [i=0,k+1] i = (k+1)((k+1)+1)/2 =>-proof
[i=0,k+1] i = (k+1)((k+1)+1)/2 =>-proof
Finally, it should be noted that induction may be done on expressions that
contain more than one variable. Under such circumstances, one of the variables
must be chosen and induction must be done only on that variable. So, to prove
 x
x y
y zP(x, y, z) by
induction on z, for example, one proves
zP(x, y, z) by
induction on z, for example, one proves
 x
x yP(x, y, 0) as the base case
and
yP(x, y, 0) as the base case
and  x
x y(P(x, y, k)=>P(x, y,
k+1)) as the inductive step. Since the x and the y in the
inductive step are universally quantified, anything can be substituted for
their occurrences in the inductive hypothesis. For example, the inductive
hypothesis in the above-mentioned proof of
y(P(x, y, k)=>P(x, y,
k+1)) as the inductive step. Since the x and the y in the
inductive step are universally quantified, anything can be substituted for
their occurrences in the inductive hypothesis. For example, the inductive
hypothesis in the above-mentioned proof of
 x
x y
y zP(x, y, z) would
be
zP(x, y, z) would
be  x
x yP(x, y, k), and this could
be applied to produce statements such as P(x+1, y, k), P(x, k,
k), P(a, b, k), &c., wherever they are needed.
yP(x, y, k), and this could
be applied to produce statements such as P(x+1, y, k), P(x, k,
k), P(a, b, k), &c., wherever they are needed.
Another peculiarity of multi-variable inductive proofs is the possibility of
employing smaller inductive proofs, with induction done on a different
variable, as sub-proofs. These sub-proofs can be termed lemmas. These
lemmas can employ their own inductive hypotheses and also the inductive
hypothesis of the main proof. Examples of multi-variable proofs and proofs
involving lemmas will be presented in the next section.
It is interesting to use logic to describe the kinds of sets to which the
method of induction applies. In this introduction we have treated dominoes in
chains, rungs on a ladder, units of water flowing into a siphon, and the
natural numbers. All these sets have a property in common that allows
induction to be used to prove assertions about them. (If the discussion that
follows is confusing to you, these paragraphs may be skipped.) The "less than"
relation on the natural numbers, symbolised by `<', is familiar to you from
algebra. There are similar relations on the dominoes, the ladder rungs, and
the units of water flowing into the siphon. On the set of dominoes, the
relation is defined by the order of the dominoes in the chain. If domino
x would fall before domino y, then x<y. On the
set of ladder rungs the relation is described by the expression "lower than".
On the units of water flowing into a siphon, the relation is one of temporal
precedence: the units of water flow into the siphon in some order in time.
Thus with any of these sets, the relation `<' can be defined on the
elements. This ordering relation is used in what follows. Recall that the
strong form of induction states that if it is true that if some property
P holds for all the elements in the set under consideration that are
less than some element y, then P must hold for y also,
then P must hold for all the elements of the set under consideration.
This can be stated formally:[25]
 xP(x) <=>
xP(x) <=>
 y(
y( x(x<y =>
P(x)) => P(y))
x(x<y =>
P(x)) => P(y))
Remember that any implication A=>B is equivalent to the statement
~A B. (In the exercises in the propositional calculus, this
identity was termed "implication reduction".) Remember also that
~
B. (In the exercises in the propositional calculus, this
identity was termed "implication reduction".) Remember also that
~ xF(x) <=>
xF(x) <=>
 x~F(x). These two theorems can be combined to
yield the theorem (
x~F(x). These two theorems can be combined to
yield the theorem ( xF(x) => B) <=>
(
xF(x) => B) <=>
( x~F(x)
x~F(x)  B). This theorem can be
applied to the right-hand side of the statement above to yield
B). This theorem can be
applied to the right-hand side of the statement above to yield
 xP(x) <=>
xP(x) <=>
 y(
y( x~(x<y =>
P(x))
x~(x<y =>
P(x))  P(y))
P(y))
Applying implication reduction in the sub-expression ~(x<y
=> P(x)) yields ~(~(x<y)  P(x)). DeMorgan's
P(x)). DeMorgan's  -Law and ~-use transform this
into x<y
-Law and ~-use transform this
into x<y  ~P(x). So the full
expression becomes
~P(x). So the full
expression becomes
 xP(x) <=>
xP(x) <=>
 y(
y( x(x<y
x(x<y
 ~P(x))
~P(x))  P(y))
P(y))
The predicate P defines a set. In fact, it defines two sets, all the
elements in the universe for which P is true and all the elements in the
universe for which P is false. We can give these sets names. Let us
call the set of all the elements of the universe for which P is false
"NOT_P". Then for any element x, "P(x)" can be rewritten
as "x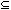 NOT_P", and "~P(x)" can be rewritten
as "x
NOT_P", and "~P(x)" can be rewritten
as "x NOT_P". Under these translations, the expression
that we are working with becomes
NOT_P". Under these translations, the expression
that we are working with becomes
 x(x
x(x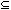 NOT_P) <=>
NOT_P) <=>
 y(
y( x(x<y
x(x<y
 x
x NOT_P)
NOT_P)  y
y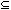 NOT_P)
NOT_P)
Now the left-hand side of this equivalence becomes recognisable as a fancy way
of stating that NOT_P is empty:
(NOT_P =  ) <=>
) <=>
 y(
y( x(x<y
x(x<y
 x
x NOT_P)
NOT_P)  y
y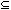 NOT_P)
NOT_P)
If both sides of a true equivalence are negated, the resulting equivalence is
true. So, again by applying quantifier negation, DeMorgan's laws, and
implication reduction, the expression can be transformed through the following
steps:
(NOT_P !=  ) <=>
~
) <=>
~ y(
y( x(x<y
x(x<y
 x
x NOT_P)
NOT_P)  y
y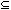 NOT_P) negation of both sides
NOT_P) negation of both sides
(NOT_P !=  ) <=>
) <=>
 y~(
y~( x(x<y
x(x<y
 x
x NOT_P)
NOT_P)  y
y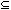 NOT_P) quantifier negation
NOT_P) quantifier negation
(NOT_P !=  ) <=>
) <=>
 y(~
y(~ x(x<y
x(x<y
 x
x NOT_P)
NOT_P)  y
y NOT_P) DeMorgan's
NOT_P) DeMorgan's  -Law (with ~-use)
-Law (with ~-use)
(NOT_P !=  ) <=>
) <=>
 y(
y( x~(x<y
x~(x<y
 x
x NOT_P)
NOT_P)  y
y NOT_P) quantifier negation
NOT_P) quantifier negation
(NOT_P !=  ) <=>
) <=>
 y(
y( x(~(x<y)
x(~(x<y)
 x
x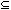 NOT_P)
NOT_P)  y
y NOT_P) DeMorgan's
NOT_P) DeMorgan's  -Law
-Law
(NOT_P !=  ) <=>
) <=>
 y(
y( x(x<y =>
x
x(x<y =>
x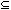 NOT_P)
NOT_P)  y
y NOT_P)
implication reduction
NOT_P)
implication reduction
This final statement is termed "well-foundedness". In English, it says that if
NOT_P is nonempty, then NOT_P must contain some element y such that all
elements of U that are less than y must be excluded from NOT_P.
Take a moment to verify this meaning in your own thoughts, and review how this
form was derived starting from the principle of strong induction.
We are interested in the question of when the method of induction applies in
general, for any property P. So, since P is an arbitrary
property, the set NOT_P is an arbitrary subset of the universe. Therefore, in
order for induction to apply to a universe U, the above statement must
hold for all subsets S of the universe U:
(S !=  ) <=>
) <=>
 y(
y( x(x<y =>
x
x(x<y =>
x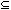 S)
S)  y
y S)
S)
A universe U with a "less than" relation < is
well-founded if and only if every nonempty subset of U contains a
minimal element with respect to the relation <. That is, no
matter how one chops up U into subsets, in any subset S one can
always find some particular element y such that there are no elements of
S that are less than y. This makes sense, intuitively.
Induction works by establishing chains of implication that grow upwards
according to the structure that is imposed on the set by the <
relation. Each of these chains must be "founded" upon some minimal element.
One can imagine arranging an infinite set of dominoes so that no chain of the
dominoes has a beginning or an end. The simplest way to do this is to place a
domino next to each integer on a number line. This arrangement has no
beginning and no end; there is no least integer and there is no greatest
integer. Note that one can use induction on subsets of this set that
are well-founded under the relation `<'. In particular, induction
applies to the natural numbers, a subset of the integers. (In fact, if we
scrap the conventional "less than" relation on the integers and arrange them in
a different way, we can use induction on them. This illustrates the
importance of the choice of `<' relation. To see some ways in which the
elements of sets can be rearranged to one's advantage, see the appendix on
infinity.) This can be viewed metaphorically as choosing a domino somewhere in
the middle of the chain that has no beginning and no end, and knocking it over.
All its successors topple. But the set on which induction is being used in
this case is not the entire chain of dominoes, but the sub-chain that begins
with the domino that was first knocked over. Thus this sub-chain is
well-founded. The example of the integers is somewhat mundane; one can also
imagine a chain of dominoes that in both directions (going toward the greater
and going toward the lesser) branches out into infinitely many side-chains,
each of which in turn branches out into infinitely many side chains, &c.
Such a structure would have no beginning and no end.
EXERCISES
- 0. Show
 n(
n(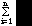 (2i-1) =
n2)
(2i-1) =
n2)
- 1. Show that for all x != 1,
 n(
n( xi = (xn+1
-1)/(x-1))
xi = (xn+1
-1)/(x-1))
- 2. Show
 n(
n( i2
= (n)(n+1)(2n+1)/6)
i2
= (n)(n+1)(2n+1)/6)
- 3. Show
 n(
n(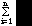 (i/(i+1)!) = 1 - 1/(n+1)!)
(i/(i+1)!) = 1 - 1/(n+1)!)
- 4. (The Oracle Problem) There once was an island inhabited by a tribe of 1000
very logical people, 800 of whom had brown eyes and 200 of whom had blue eyes.
Mirrors and other reflecting surfaces (and any other nitpick that can screw up
this problem) were prohibited on the island, and discussion of eye colour was
tabooed. According to tribal law, if anyone could prove that their eyes were
blue, then at the following midnight that person had to kill themselves. The
tribal god, who was, of course, infallible, spoke through an oracle on the
island, and one day this oracle gave the people the following pronouncement:
"There are blue-eyed people on this island." What happened, and why?
- 5. The oracle in the previous problem stated something already known to
everyone on the island. Why, then, was its statement significant?
- 6. What is wrong with the following inductive "proof" that all horses are the
same colour? (Think about what assumptions are being made about properties
applying to horses.)
Base case: One horse is the same colour as itself.
Inductive case:
Assume that k horses are the same colour. Show k+1 horses are
the same colour
Remove one horse from the group of k+1 horses.
The remaining k horses are the same colour. inductive hypothesis
Put that horse back, remove another horse.
The remaining k horses are the same colour. inductive hypothesis
So, by transitivity, all k+1 horses must be the same colour.
Therefore, all horses are the same colour.
Induction on Lists
A list is a sequence of objects. The simplest possible list is the empty list
( ), which can also be denoted using the special word nil. The set of
lists can be inductively defined, with nil as the base:
( )  LISTS
LISTS
 x
x (y1 ... yn) ( (y1 ... yn)
(y1 ... yn) ( (y1 ... yn)  LISTS
=> (x y1 ... yn)
LISTS
=> (x y1 ... yn)  LISTS ) where (y1 ... yn) is a list of
0 or more elements
LISTS ) where (y1 ... yn) is a list of
0 or more elements
All lists can be generated by a chain of applications of the above rules.
Nothing that cannot be derived using the rules is a list.
Anything that is not a list is called an atom. Note that in the above
definition, x (called the "head" of the list) may be anything in the
universe, but (y1 ... yn) (called the "tail" of the list) must be a
list. Thus the construction of lists is right-recursive; the right-hand
part of a list must itself be a list. Since there are no constraints on the
nature of the left-hand element, it may or may not be a list itself. The
left-hand element of the list ((Heraclitus) Parmenides Zeno) is the list
(Heraclitus). The left-hand element of the list (Democritus Dalton Fermi) is
the atom Democritus. Lists may be viewed as syntax trees, just as
formulæ from the propositional and the predicate calculi may be viewed as
syntax trees.
Here are some more lists and their heads and tails:
LIST HEAD TAIL
(((1) 1) A) ((1) 1) (A)
(1 1 (A (2 (B)))) 1 (1 (A (2 (B))))
(1 (B (2) B) 3) 1 ((B (2) B) 3)
((0 0 0) DESTRUCT (0)) (0 0 0) (DESTRUCT (0))
Remember, the left-hand element may be an atom, but the right-hand element of
any list is always another list.
We can define some interesting functions over the set of lists. In the
following definitions, `x', `y', and `z' represent lists,
and `n' represents an atom or a list.
append-base:  y(append(nil, y) = y)
y(append(nil, y) = y)
append-step:
 n
n y
y z(append((n
y), z) = (n append(y, z)))
z(append((n
y), z) = (n append(y, z)))
reverse-base: reverse(nil) = nil
reverse-step:  n
n y(reverse((n y))
= append(reverse(y), (n)))
y(reverse((n y))
= append(reverse(y), (n)))
The names of the functions are mnemonic; append concatenates two lists, and
reverse reverses the elements of a list (but not the elements of any
sub-lists). Try out append and reverse on some sample lists of
your own choosing, and see how they operate. Once you've done this, you'll be
ready for some theorems:
Right identity for append: Show  x append(x, nil) =
x
x append(x, nil) =
x
base case: x = nil
append(nil, nil) = nil append-base (left identity)
inductive step: x = k
[assume append(k, nil) = k Show append((n k), nil) =
(n k)
append((n k), nil) = (n append(k, nil)) append-step
= (n k) ] inductive hypothesis
append(k, nil) = k => append((n k), nil) = (n
k) =>-proof
Associativity of append: Show
 x
x y
y z(append(x,append(y,
z)) = append(append(x, y), z))
z(append(x,append(y,
z)) = append(append(x, y), z))
base case: x = nil; choose arbitrary y, z.
append(nil, append(y, z)) = append(y, z) append-base
= append(append(nil, y), z) append-base
Therefore  y
y z(append(nil, append(y,
z)) = append(append(nil, y), z)), by
z(append(nil, append(y,
z)) = append(append(nil, y), z)), by  -proof.
-proof.
inductive step: x = k
[assume  y
y z(append(k,
append(y, z)) = append(append(k, y), z)) Show
z(append(k,
append(y, z)) = append(append(k, y), z)) Show
 y
y z(append((n k), append(y,
z)) = append(append((n k), y), z))
z(append((n k), append(y,
z)) = append(append((n k), y), z))
choose arbitrary y, z:
append((n k), append(y, z)) = (n append(k,
append(y, z))) append-step
= (n append(append(k, y), z)) inductive hypothesis
= append((n append(k, y)), z) append-step
= append(append((n k), y), z) append-step
Therefore  y
y z(append((n k),
append(y, z)) = append(append((n k), y), z)), by
z(append((n k),
append(y, z)) = append(append((n k), y), z)), by
 -proof. ]
-proof. ]
 y
y z(append(k, append(y,
z)) = append(append(k, y), z)) =>
z(append(k, append(y,
z)) = append(append(k, y), z)) =>
 y
y z(append((n k), append(y,
z)) = append(append((n k), y), z)) =>-proof
z(append((n k), append(y,
z)) = append(append((n k), y), z)) =>-proof
Distributivity of reverse over append: Show  x
reverse(append(x, y)) = append(reverse(y),
reverse(x))
x
reverse(append(x, y)) = append(reverse(y),
reverse(x))
base case: x = nil; choose arbitrary y.
reverse(append(nil, y)) = reverse(y) append-base
= append(reverse(y), nil) right identity for append
= append(reverse(y), reverse(nil)) reverse-base
Therefore,  y(reverse(append(nil, y)) =
append(reverse(y), reverse(nil))), by
y(reverse(append(nil, y)) =
append(reverse(y), reverse(nil))), by  -proof.
-proof.
inductive step: x = k
[assume  y(reverse(append(k, y)) =
append(reverse(y), reverse(k))) Show
y(reverse(append(k, y)) =
append(reverse(y), reverse(k))) Show
 y(reverse(append((n k), y)) =
append(reverse(y), reverse((n k))))
y(reverse(append((n k), y)) =
append(reverse(y), reverse((n k))))
choose arbitrary y:
reverse(append((n k), y)) = reverse((n append(k,
y))) append-step
= append(reverse(append(k, y)), (n)) reverse-step
= append(append(reverse(y), reverse(k)), (n)) inductive
hypothesis
= append(reverse(y), append(reverse(k), (n)))
associativity of append
= append(reverse(y), reverse((n k))) reverse-step
Therefore,  y(reverse(append((n k), y)) =
append(reverse(y), reverse((n k)))), by
y(reverse(append((n k), y)) =
append(reverse(y), reverse((n k)))), by  -proof.
]
-proof.
]
 y(reverse(append(k, y)) = append(reverse(y),
reverse(k))) =>
y(reverse(append(k, y)) = append(reverse(y),
reverse(k))) =>  y(reverse(append((n k),
y)) = append(reverse(y), reverse((n k)))) =>-proof
y(reverse(append((n k),
y)) = append(reverse(y), reverse((n k)))) =>-proof
Remember, you can do induction on only one variable at a time! If you have two
variables x and y, and you are doing induction on x, then
y is arbitrary; don't touch it. When proving a result involving more
than one variable, you may start by doing induction on one variable and then
find that you reach an impasse. You can either try starting with induction on
the other variable or try to prove by induction on the other variable a lemma
that will allow you to continue. Finally, remember to look for places to use
the inductive hypothesis. Many students feel that they are stuck because they
cannot find any definitions or theorems that would usefully transform an
expression that they have derived, when in actuality the answer is staring them
in the face in the form of the inductive hypothesis that they have written down
at the beginning of the proof. Writing an inductive proof is like starting on
one bank of a river and using a bridge to reach a point directly across the
river, on the opposite bank: One must first walk along the river in order to
get to the bridge. Although this seems to bring one farther from one's
destination and to make the problem more complex, it is a necessary step,
because the opposite bank can be reached only by crossing the bridge. Once one
has crossed the bridge, one may walk along the river in the opposite direction
in order to reach one's destination on the far side. The bridge is analogous
to the inductive hypothesis. An inductive proof massages an antecedent
expression into a form to which the inductive hypothesis applies, then uses the
inductive hypothesis, and then massages the result into the form that is
demanded as the consequent.
We can define a function from lists to natural numbers called length,
as follows:
length-base: length(nil) = 0
length-step: length((n y)) = 1+length(y)
This function computes the length of a list.
EXERCISES
- 0. Show
 x
x y(length(append(x, y))
= length(x)+length(y))
y(length(append(x, y))
= length(x)+length(y))
- 1. Show
 x(length(reverse(x)) = length(x)).
x(length(reverse(x)) = length(x)).
- 2. Let the operation sum be defined as follows:
sum-base: sum(nil) = 0
sum-step: sum(n x) = n+sum(x)
Show  x
x y(sum(append(x, y)) =
sum(x)+sum(y)).
y(sum(append(x, y)) =
sum(x)+sum(y)).
- 3. There is more than one way to reverse a list. Let rev' and revz operate as
follows:
rev'-0: rev'(x) = revz(x, nil)
rev'-1: revz(nil, x) = x
rev'-2: revz((n x), y) = revz(x, (n y))
Show  x
x y(revz(x, y) = append(rev(x),
y)).
y(revz(x, y) = append(rev(x),
y)).
- 4. Use the theorem established in the previous exercise to show that
rev' and rev are equivalent; that is, show
 x(rev'(x) = rev(x)).
x(rev'(x) = rev(x)).
Peano Arithmetic
However strange it may seem to you at first, the natural numbers are a lot
like lists. The natural numbers were given an inductive definition and
symbolisation and a formal system of inference by the Italian mathematician
Peano. This system rests upon the idea of the successor function. Taking the
successor of a natural number is like incrementing it by 1. Here is Peano's
inductive definition of the set N, the natural numbers:
0  N (0 is a natural number.)
N (0 is a natural number.)
 x(x
x(x  N => sx
N => sx
 N) (The successor of any natural number is a natural
number.)
N) (The successor of any natural number is a natural
number.)
 x
x y(x
y(x  N
N  y
y  N
N  x!=y => sx
!= sy) (No two natural numbers have the same successor.)
x!=y => sx
!= sy) (No two natural numbers have the same successor.)
~ x(sx = 0) (0 is not the successor of any number.)
x(sx = 0) (0 is not the successor of any number.)
Any property that is possessed by 0, and also by the successor of any number
that possesses it, is possessed by all the natural numbers.
Simpler definitions of the natural numbers have since been constructed, but
Peano's will suffice for our purposes. Note that Peano's final property is
only the principle of weak induction. The unary operator `s' means "successor
of". So the string of symbols "s0" in the Peano system refers to the idea that
is expressed in English by the word "one". "ss0" has the same meaning as
"two", "sss0" the same meaning as "three", and so on. The symbol `0' is the
base element, corresponding to nil in the lists world. It is easy to
see that any natural number n is expressed in Peano arithmetic by
stacking n `s's in front of a `0'. This may seem circular, depending
upon your point of view--I've just used numbers and counting to describe a way
to implement numbers and counting. One can't think of n `s's without
implicitly referring to numeration. But in a way the Peano axioms say nothing
about counting: all that they describe is the successor function, a way of
shunting around strings of `s's. Their implementing counting is a sort of side
effect. We can introduce Arabic numerals as meta-symbols to make it easier to
write out numbers in Peano arithmetic: "sn", where
n is an Arabic numeral, can be taken as a shorthand for a string of n
`s`s. Parentheses can be included in Peano arithmetic expressions in the
same way that they are employed in everyday arithmetic. Strictly speaking, the
formalism should include rules to implement parenthesisation if there are going
to be parentheses in formulæ, but I feel that explicit parenthesisation
rules would only obstruct and confuse the student. You should, however, be
aware that expressions that are not fully parenthesised are only shorthand
notation for expressions that are. So the shorthand
"s30.s0+s20" really means
"((s(s(s(0))).s(0))+s(s(0)))". The appearance and disappearance of parentheses
because of operator precedences often causes problems for students who try to
substitute one expression for another. Suppose that one is working with the
expression x.y, and it has been discovered that x =
a+b. Then the result of the substitution must include
parentheses in order to generate the correct order of operations:
(a+b).y. This case arises in everyday algebra. A case
more often overlooked is that of substituting a sum into a sum or a product
into a product. Here parentheses must be employed to resolve the ambiguity in
order of operations. (Most systems give binary arithmetic operators such as +
and . left association, that is, an unparenthesised expression such as
x+y+z defaults to left-to-right evaluation:
(x+y)+z. For our purposes, however, it is best to be
explicit.) When dealing with parenthesisation, think not of substituting one
string of symbols for another but of grafting one syntax tree into the place of
another. When operator precedences do not lead to the correct syntax tree,
they must be overridden using parenthesisation. This view will lead to
appropriate parenthesisation.
In the lists world there is an infinite number of successors for each list,
although every list (except nil) has a unique predecessor. The
successors of list x are all represented by (n x), with n
standing for an arbitrary element of the universe. In the world of Peano
arithmetic there is only one possible successor for each number. There are,
however, many similarities. Identities, associativities, and distributivities
exist in both the list world and the Peano arithmetic world. Here are the
axioms for arithmetic in the Peano world:
plus-base:  x(x+0 = x)
x(x+0 = x)
plus-step:  x
x y(x+s(y) =
s(x+y))
y(x+s(y) =
s(x+y))
mult-base:  x(x.0 = 0)
x(x.0 = 0)
mult-step:  x
x y(x.s(y)
= x +x.y)
y(x.s(y)
= x +x.y)
The operations + and . are self-explanatory, coming as they do from simple
arithmetic. The plus-base and mult-base rules are right additive identity and
right multiplicative zero. The left identity and left zero properties can be
proven as theorems. The plus-step rule is the equivalent of the commutation
x+(y+1) = (x+y)+1. The mult-step rule is the
equivalent of the distribution and commutation x.(y+1) = x
+ x.y. Here are some proofs.
Show s20+s20 =
s40: i.e., show that 2+2=4
s20+s20 =
s(s20+s0) plus-step
= s2(s20+0) plus-step
= s2s20 =
s40 plus-base
Show  x(x+s(0) = s(x)):
x(x+s(0) = s(x)):
x+s(0) = s(x+0) plus-step
= s(x) plus-base
Therefore,  x(x+s(0) = s(x)) by
x(x+s(0) = s(x)) by
 -proof.
-proof.
Show  x(x.s(0) = x): right multiplicative
identity
x(x.s(0) = x): right multiplicative
identity
x.s(0) = x + x.0 mult-step
= x+0 mult-base
= x plus-base
Therefore,  x(x.s(0) = x) by
x(x.s(0) = x) by
 -proof.
-proof.
Show  x(0+x = x) left additive identity
x(0+x = x) left additive identity
base case: x = 0
0+0 = 0 plus-base
inductive step: x = k
[assume 0+k = k Show 0+s(k) = s(k)
0+s(k) = s(0+k) plus-step
= s(k) ] inductive hypothesis
0+k = k => 0+s(k) = s(k) =>-proof
Lemma:  x
x y(s(x+y) =
s(x)+y) needed in proof of commutativity of +
y(s(x+y) =
s(x)+y) needed in proof of commutativity of +
base case: y = 0; choose arbitrary x.
s(x+0) = s(x) plus-base
= s(x)+0 plus-base
inductive step: y = k
[assume  x(s(x+k) = s(x)+k)
Show
x(s(x+k) = s(x)+k)
Show  x(s(x+s(k)) = s(x)+s(k))
x(s(x+s(k)) = s(x)+s(k))
choose arbitrary x:
s(x+s(k)) = s2(x+k)
plus-step
= s(s(x)+k) inductive hypothesis
= s(x)+s(k) plus-step
Therefore,  x(s(x+s(k)) =
s(x)+s(k)), by
x(s(x+s(k)) =
s(x)+s(k)), by  -proof. ]
-proof. ]
 x(s(x+k) = s(x)+k) =>
x(s(x+k) = s(x)+k) =>
 x(s(x+s(k)) = s(x)+s(k))
=>-proof
x(s(x+s(k)) = s(x)+s(k))
=>-proof
Show  x
x y(x+y =
y+x) commutativity of +
y(x+y =
y+x) commutativity of +
base case: y=0; choose arbitrary x.
x+0 = x plus-base
= 0+x left additive identity
Therefore,  x(x+0 = 0+x), by
x(x+0 = 0+x), by
 -proof.
-proof.
inductive step: y=k
[assume  x(x+k = k+x) Show
x(x+k = k+x) Show
 x(x+s(k) = s(k)+x)
x(x+s(k) = s(k)+x)
choose arbitrary x:
x+s(k) = s(x+k) plus-step
= s(k+x) inductive hypothesis
= s(k)+x lemma
Therefore,  x(x+s(k) =
s(k)+x), by
x(x+s(k) =
s(k)+x), by  -proof. ]
-proof. ]
EXERCISES
Remember, you can employ any theorem that you have proven previously as a step
in the proof of a new theorem. Also, remember to use your inductive
hypothesis. Finally, you can check your work by noting that "s(x)" acts
like "x+1"; if you begin with s(x)+s(y) and get
s(x+y), for example, you know that you have goofed somewhere
along the way, because (x+1)+(y+1) != (x+y)+1.
- 0. associativity of addition:
 x
x y
y z((x+y)+)
= x+(y+z))
z((x+y)+)
= x+(y+z))
- 1. left multiplicative zero:
 x(0.x = 0)
x(0.x = 0)
- 2.
 x
x y(x+y.x =
s(y).x)
y(x+y.x =
s(y).x)
- 3. commutativity of multiplication:
 x
x y(x.y = y.x) (Try
induction on y.)
y(x.y = y.x) (Try
induction on y.)
- 4. distributivity:
 x
x y
y z(x.(y+z)
= x.y + x.z)
z(x.(y+z)
= x.y + x.z)
NEXT CHAPTER: 2. Language
[11][Carroll 1936] p. 181.
[12]Stephen Kandel, "I, Mudd" episode of Star Trek.
Paramount, 1967.
[13][Harper 1904] p. 99-101.
[14][Harper 1904] p. 51.
[15][Quetelet 1848] p. 301.
[16][Quetelet 1835] p. 98-99.
[17][Porter 1986]
[18][Galton 1907]
[19][Dubbey 1977], [Becher 1980]
[20][Dubbey 1977]
[21][Pycior 1981]
[22][Boole 1854]
[23]A worm is an independent program capable of initiating
an infection on its own. A virus, in contrast, resides within another program
and is potent only when that program is executed.
[24][Gries 1981]
[25]The proof that follows is from [Gries 1987].
 (x=54))' would be a legal proposition.) Compound
propositions can be built from other compound propositions and atoms using the
connectives. Here is a table of connectives and their meanings.
Incompatibility is denoted by the operator `/', which can be read as "is
incompatible with".
(x=54))' would be a legal proposition.) Compound
propositions can be built from other compound propositions and atoms using the
connectives. Here is a table of connectives and their meanings.
Incompatibility is denoted by the operator `/', which can be read as "is
incompatible with".

 ' and `
' and ` ', the
universal and existential quantifiers. A proposition can be quantified by
preceding it with one or more quantifiers. The universal quantifier
`
', the
universal and existential quantifiers. A proposition can be quantified by
preceding it with one or more quantifiers. The universal quantifier
` '0'..'9' ->
'0'..'9' -> i = (n)(n+1)/2) by
weak induction:
i = (n)(n+1)/2) by
weak induction: [i=0,0] i = 0
[i=0,0] i = 0 NOT_P", and "~P(x)" can be rewritten
as "x
NOT_P", and "~P(x)" can be rewritten
as "x ) <=>
) <=>
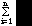 (2i-1) =
n2)
(2i-1) =
n2)